Werden wir Helden für einen Tag

Random R code to teach statistics #1 k x 2 x 2 array

Posted on Dec 16, 2012 by Chung-hong Chan

問題來自 Hong Kong R Usergroup 。對！竟然是有人 post 問題，雖然問問題的人我是認識的，要多謝她去撐場。問題是 mantelhaen.test (Mantel-Haenszal test) 如何解讀，主要解答部份是後續的分析。用內建的 UCBAdmissions ，可以說明此類 k x 2 x 2 array 的問題。

UCBAdmissions 問題是經典的統計學問題，清楚說明何謂 Simpson's Paradox 。這 dataset 是柏克萊大學 73 年的入學統計，是男女申請人的取錄比率。

# Chainsaw Riot http://www.chainsawriot.com k22 problem
# pooled 2x2 table and pooled odds ratio
apply(UCBAdmissions, c(2, 1), sum)
fisher.test(apply(UCBAdmissions, c(2, 1), sum))

# stratum-specific odds ratio
apply(UCBAdmissions, 3, function(x) fisher.test(x)$estimate)
# stratum-specific admission rate and gender prevalence
apply(UCBAdmissions, c(1, 3), sum)/apply(UCBAdmissions, 3, sum)
apply(UCBAdmissions, c(2, 3), sum)/apply(UCBAdmissions, 3, sum)
# meta-analysis using metafor
require(metafor)
meta.obj <- rma.mh(ai = UCBAdmissions[1, 1, ], bi = UCBAdmissions[1, 2, ], ci = UCBAdmissions[2, 1, ], 
	di = UCBAdmissions[2, 2, ], slab = letters[1:6])
meta.obj
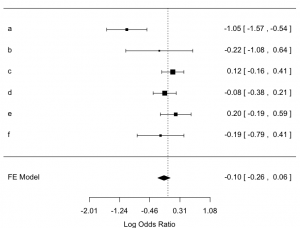
plot(meta.obj)
#loglinear model
require(MASS) #built-in
fm.loglm <- glm(Freq~Dept*Admit*Gender, data=as.data.frame(as.table(UCBAdmissions)), family=poisson)
summary(fm.loglm) # Dept * Admit * Gender are significant in some cases

第三行：結果如此

        Admit
Gender   Admitted Rejected
  Male       1198     1493
  Female      557     1278

單看數字，看來柏大男生的取錄比率較高，有性別歧視之嫌。
如果計算 odds ratio ((例如用 fisher.test 這個 function)) ，可計出 odds ratio 高達 1.84 (95% CI 1.62 to 2.09) 。
但是，那 set data 是有分開不同 department 的 2x2 table 。若果每個 dept 都計一次 odds ratio 可得出以下結果（第七行）:

        A         B         C         D         E         F 
0.3495628 0.8028124 1.1329004 0.9213798 1.2211852 0.8280944

由此可見，各 department 的男女收生機會都有所不同，故此將各個部門的數據統合在一起 (pool) 來分析並不洽當。
至於為何統合分析後看上去有性別歧視的假像。那就可以看一些 descriptive statistics 。先看看各個部門的取錄比率，以及各部門的男女申請比例。（九、十行）
結果

          Dept
Admit              A         B         C         D         E          F
  Admitted 0.6441586 0.4030501 0.5513699 0.2883173 0.1601307 0.07876712
  Rejected 0.5675214 0.2714646 0.8347339 0.8940171 0.5517677 0.93557423

        Dept
Gender           A          B         C         D         E         F
  Male   0.8842444 0.61002179 0.5565068 0.4469453 0.2080610 0.6386986
  Female 0.1846154 0.03156566 0.8305322 0.6410256 0.4962121 0.4775910

從以上表可見，不論性別，部門 C, D, F 的取錄率很低。而同時女性亦較常去申請入讀 C, D, F 部門，故此得出以上假像。
問題是如何測試各個 strata (department) 的 odds ratio 是否一致。 ( homogeneity of odds ratio across strata ) ((用流行病學的語言，如果 pooled odds ratio 明顯與 stratum-specific odds ratios 不同。而 stratum-specific odds ratios 是 homogeneous 的話，那 stratum 那 variable 是 confounding factors 。))
這個問題最少可有兩個方法解決。第一是將問題轉為 meta-analysis ，用 meta-analysis 的 heterogeneity test (Tarone's Test for Heterogeneity)。

另一方法是轉為 loglinear model ，測試 admission * gender 的 association 是否與 admission 有關。