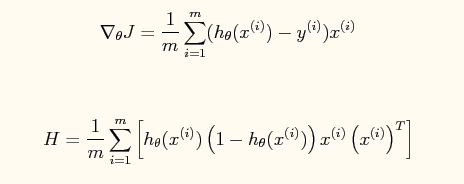chainsawriot

Newton-Raphson #2

Posted on Dec 30, 2011 by Chung-hong Chan

上回講到 Newton-Raphson 可用於取代 Gradient Descent ，今次一起看 Logistic Regression 的例子。
再用上次的 mtcars 數據，假設我想以車輛重量和汽油消耗量汽車去估計汽車的變速器類型(自動波/手動)。由於 response variable 是 binary ，故此此為 Logistic Regression 問題。有關 Logistic Regression 的 Gradient Descent 方法，不再詳講，可看 Andrew Ng 教授的 Slide [s3.amazonaws.com] 。
問題是怎樣用 Newton-Raphson 方法解決 Logistic Regression 問題。上回提過 Newton-Raphson 的 general equation

θ_n+1 = θ_n - (f(θ_n)/f'(θ_n))

從 gradient descent 的 formula 可知，每次 θ 更新時，其實是減去了 learning rate * gradient 。

[www.chainsawriot.com]

gradient 是 Cost function 的 partial derivative (f')。如果要用 Newton-Raphson ，就要找出 Cost function 的 f'' 。 f'' 計出來的東西，叫做 Hessian matrix [en.wikipedia.org] 。我的 multivariate calculus 很屎，以下是別人計出來的 f' 和 f'' 。

[www.chainsawriot.com]

而每次 iteration 更新 θ 的算法就是

[www.chainsawriot.com]

根據以上算式，寫成的 R Code 是：

## Newt logistic
y <- mtcars$am
x <- as.matrix(cbind(mtcars$mpg, mtcars$wt))
X <- cbind(rep(1, nrow(x)), x)
initheta <- matrix(c(0,0,0), ncol=1)

g <- function(z) {
    1/(1+exp(-z))
}

computeJ <- function(y,X,theta) {
  htheta <- g(X %*% theta)
  J <- (1/length(y))*sum((-y*log(htheta))-((1-y)*log(1-htheta)))
  return(J)
}

gradDescLogisticReg <- function(y, X, theta,alpha=0.01,iters=1000, Jplot=FALSE) {
  m <- length(y)
  JHist <- c()
  for (i in 1:iters) {
    htheta <- g(X %*% theta)
    gradient <- 1/m * t(X) %*% (htheta-y)
    newtheta <- theta - alpha*gradient
    JHist <- append(JHist, computeJ(y,X, newtheta))
    theta <- newtheta
  }
  if (Jplot){
  plot(JHist, type="l")
}
  return(list(theta=theta, JHist=JHist))
}

newtLogisticReg <- function(y, X, theta, iters=1000, Jplot=FALSE) {
  m <- length(y)
  JHist <- c()
  for (i in 1:iters) {
    htheta <- g(X %*% theta)
    gradient <-  1/m * t(X) %*% (htheta-y)
    hessian <- 1/m * t(X) %*% X * diag(htheta) * diag(1-htheta)
    newtheta <- theta - solve(hessian) %*% gradient # hessian may not be invertable, use ginv()
    JHist <- append(JHist, computeJ(y,X, newtheta))
    theta <- newtheta
  }
  if (Jplot){
  plot(JHist, type="l")
}
  return(list(theta=theta, JHist=JHist))
}

benchmark <- coef(glm(mtcars$am~mtcars$mpg+mtcars$wt, family=binomial()))

# will not converge!
#GD <- gradDescLogisticReg(y, X, initheta, alpha=0.1, iters=10000)$theta

#will scaling improve?
#scaled benchmark

y <- mtcars$am
scx <- as.matrix(scale(cbind(mtcars$mpg, mtcars$wt)))
scX <- cbind(rep(1, nrow(scx)), scx)
#scaled benchmark
scbenchmark <- coef(glm(y~scX[,2:3], family=binomial()))

scGD <- gradDescLogisticReg(y, scX, initheta, alpha=0.1, iters=10000)
newtLR <- newtLogisticReg(y, X, initheta)
scnewtLR <- newtLogisticReg(y, scX, initheta)
plot(scnewtLR$JHist, type="l", ylim=c(0.26, 0.5), ylab="Cost", xlab="No of iterations")
lines(scGD$JHist[1:1000], col="red")
legend("topright", legend=c("Newton-Raphson","Gradient Descent"), col=c("black", "red"), lty=c(1,1), box.col="white")
#>

從實驗可見，如果用傳統的 gradient descent ，而 X 沒有 scale 的話，根本就不能 converge 。 ((可能需要更多的 iterations 或要調整 learning rate ，但我試過 iters 在十萬以下的不同的組合，一係不能 converge ，一係就 diverge 。)) 如果將 X 作 feature scaling 的話，會在一萬次 iterations 之內 converge 。
但是，如用 Newton-Raphson method ，無論 X 有否作 feature scaling ，都可以 converge ，而且是在五十次 iterations 之內完成。
Newton-Raphson 也比 gradient descent 有多一個優點，就是不用設定 learning rate 。雖然 Newton-Raphson 有如此多的好處，但需要注意每次 iteration 的 computational cost 。 Gradient Descent 每次 iteration 是 O(no of features) ，但是 Newton-Raphson 每次 iteration 是 O(no of feature³) 。