chainsawriot
Home | About | ArchiveP-value, again and again.
Held L. A nomogram for P values. BMC Medical Research Methodology 2010, 10:21
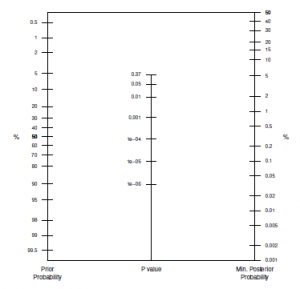
這篇文是作者是一個天才。他的天才不是在於他研究的奇特,而是在於他對世情的觀察。他明確的知道,世人是不太會接受 Bayesian Statistics , ((雖然人人都知道統計學的未來是在 Bayesian 。)) 也知道一般非統計學人對統計學的一知半解。與其教他們甚麼計算法,不如教看圖算。當年都是一樣,專貴的醫生根本不知道那些 Diagnostic test 報告上的 Sensitivity, Specificity 等等是甚麼意思,更加別說甚麼 Likelihood ratio 。後其因為出現了所謂 Fagan nomogram , Likelihood ratio 才被人所接受,甚至有取代所謂 SSPN ((Sensitivity, Specificity, Positive Predictive Value, Negative Predictive Value )) 之勢。今天這個 P-value 的 nomogram ,極有可能消滅 P-value 霸權。 ((這句很黃世澤。)) 因為 P-value 從此只會成為一個 Likelihood Function ,可輕易用來修正人們的 prior probability 。文中有個例子,例如本來你對某事的 Null hypothesis的 prior probability (類似對 Null hypothesis 成立的信心)是 10% ,後來做一個 placebo-controlled trial 得出 two-sided P-value 是 0.003 ,用 nomogram 轉換得出 Minimal posterior probability 0.5% 。即是話,有了這個實驗結果之後,我對 Null Hypothesis 成立的信心由 10% 減至 0.5% 。
這個 nomogram 可以輕易的轉為 R function ,以下是用 15 分鐘寫成的版本:
# < - Break it, Wordpress.
# P-value nomogram by Held.
# Coded by Chainsaw Riot (http://www.chainsawriot.com)
# I think I need to add some check function to p and q
BF <- function(p){
if(p < 1/exp(1)) return((-exp(1))*p*(log(p))) else return(1)
}
MPP <- function(p,q) {
(1+(((BF(p) * q)/(1-q))**-1))**-1
}
# To calculate the example above
# MPP(p=0.003, q=0.10)