chainsawriot
Home | About | ArchiveBoxplot
有護士問我,這張圖怎樣看。
Stat 101 說,這圖叫做 Boxplot ,也叫 box-and-whisker diagram 。這個圖是由 Tukey 發明。可是, Stat 101 講完 boxplot 多數是直跳去講 Statistical Test ,而沒有好好的講講 Tukey 那套 Exploratory data analysis 。故此,這些圖多數是在分析之後才畫,搞笑!
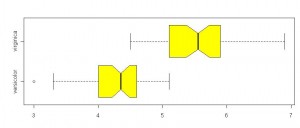
這圖展示了兩種花的 Petal 長度。以 versicolor 為例,黃色盒子的兩端,分別是 25 及 75 百分位數 ((Percentile , 25 及 75 百分位數又稱 Q1 及 Q3)) ,又稱 Lower 及 upper quartile 。圖中所見, versicolor 的 25 至 75 百分位數約為 4 至 4.6 ,可計出四份差 ((Interqurtile Range, IQR 。即 Q3-Q1)) 約是 4.6-4 = 0.6 。盒子中間的粗線,是中位數,即 50 百分位數,約為 4.3 。盒子撐出來的兩隻腳,是最大的非離群值 (largest non-outlier observation) 。即是,這個數是在 25 百分位減 1.5 個四份差及 75 百分位加1.5 個四份差之內的最大觀測值。 ((Q1 - 1.5 IQR, Q3 + 1.5 IQR 。例如 Q1 - 1.5 IQR 等於 10 ,而數據有 9 及 11 ,那麼腳就是在 9 ,而 11 是 outlier 。)) Tukey 叫這個作 sample maximum 及 sample minimum 。任何數值在這對腳以外的,就是離群數據 ((outlier)) 。 versicolor 有一個離群數據,是 3 。有時會見到有離群數據用米字型表示,那些是極端離群數據,是超過了 25 及 75 百分位數三個四份差。
這個圖表達了 Tukey 提倡的 five-number summaries ,即 sample minimun, lower quartile, median, upper quartile 及 sample maximum 。另外,中間粗線側向 lower 還是 upper quartile ,可定奪數據是否有 skewness 。如 versicolor 的中粗線微微靠近 upper quartile .數據有可能歪向高值。這個圖是 non-parametric 的,對數據的分佈沒有任何假設。
較為少見是盒子的切口( notch ),這個是 Tukey 後來提倡的。切口的位置.是 Tukey 以無母數假設計出來,類近中位數的 95% CI 。計法是
Median +/- 1.7 (1.25 IQR / 1.35 SQRT(N))
Tukey 認為,如果兩個盒子的切口沒有重疊,代表兩者的 median 應該不相同。如圖中的 versicolor 及 virginica 的盒子切口沒有重疊,似乎代表兩者的 median 有不同,可引領做一點 statistical test ,如 Median test 或 Mann-Whitney 。