Werden wir Helden für einen Tag

Home | About | Archive

---

Linear Mixed model using R: a quick primer

Posted on Oct 19, 2008 by Chung-hong Chan

在博客寫這些的東西，我想只有傻瓜才會做。
但其實博客的功能是反映我最近的 focus obsession 。與其寫最近的 focus obsession 是些悲傷的東西，不如寫寫最近私下研究的東西，叫做 Linear Mixed Effect Model （ lme ）。
〔警告：這篇東西非常長，而對一般的讀者甚至一般統計學者來說，作用不太大。除非你有興趣了解 Linear Mixed Model ，否則請別浪費時間在這篇文章。在 RSS Reader 選 read 再看其他博客吧。〕
LME 是甚麼，不太想詳談，維基百科有相當詳細的解釋。只想拿出三句。方差分析（ ANOVA ）應該有三個層次（ Model I, II, III），分別是固定作用模型（ Fixed effect model ）、隨機作用模型（ Random Effect model ）和混合作用模型（ Mixed Effect ）。固定作用模型是指數據是從一常態分佈的母體中抽樣獲得，如果要比較兩組人，他們唯一的分別只會是其平均數。隨機作用模型是指數據只是一個百鳥歸巢的聚集，其實數據是來自不同的母體。要比較兩組人的話，其差別會受制於「百鳥歸巢」的聚集分佈。混合作用模型是指，固定及隨機的因素同時存在。傳統的 Least square Regression （ OLS Regression ）只會處理固定作用因素，因為這些模型假定每個數據是獨立的。
有不少情況 OLS 不是合適的分析方法，例如數據是從同一個人收集幾次。這些情況要用到混合作用模型。 ((之前有講過相關的東西))
用上課時用到的一個例子（數據可到中大流行病學及生命統計學中心統計電算網站下載，叫做 dental.sav ），此研究想了解年紀與某兩器官的距離（ dist ）之關係。有一班小朋友，由 8 至 14 歲跟進了他們數年，每年量度一次 dist 。我們不能就此用 OLS regression 來分析年齡及 dist 之關係，因為這會違反獨立觀測假設。我們要考慮到每個小朋友都會提供幾個數據，這個就是 random effect 「百鳥歸巢」的意義。我們亦都相信每個小朋友生長的速度都有所不同。雖然有一個平均的生長速度，但每個人的生長速度有微妙的分別，都會影響整體年齡和 dist 的關係。
我不想講太多 Mixed effect 的背後理論，只想講出研究多日來，發現一些 LME 應用時非常重要的問題。我甚至去信教授們有關的問題，但我沒有收到一個滿意答案， ((Well. 講得衰一點，其實身邊那麼多人，在學業上有問題，第一個要問的，應是教你的人。不是因為他們教你，只因為他們其實受薪答你問題，而教你的人的薪水你有份給他。)) 只好自行尋覓。這些問題，會在我們的例子中見到。請使用最新版本的 R ，而使用的套位也請更新。

先用 foreign 套件載入 spss 格式數據檔案 dental.sav

>library(foreign)
>den.data < - read.spss(file.choose(),to.data.frame=TRUE)
我們先看看數據，已經用 data frame 形式載入到 R 。我們看看頭 10 個數據。
>den.data[1:10,]
V1 id age dist gender
1 2 1 10 20.0 0
2 3 1 12 21.5 0
3 4 1 14 23.0 0
4 5 2 8 21.0 0
5 6 2 10 21.5 0
6 7 2 12 24.0 0
7 8 2 14 25.5 0
8 9 3 8 20.5 0
9 10 3 10 24.0 0
10 11 3 12 24.5 0

也可用 str() 看看數據的 summary 。

>str(den.data)
'data.frame': 108 obs. of 5 variables:
$ V1 : num 2 3 4 5 6 7 8 9 10 11 ...
$ id : num 1 1 1 2 2 2 2 3 3 3 ...
$ age : num 10 12 14 8 10 12 14 8 10 12 ...
$ dist : num 20 21.5 23 21 21.5 24 25.5 20.5 24 24.5 ...
$ gender: num 0 0 0 0 0 0 0 0 0 0 ...
V1 只是行數，可以不理。 id 是小朋友的假名， age 是年紀， dist 是 outcome variable ， gender 是性別。數據初步見到，每個小朋友都在不同的歲數提供幾個 dist 的數據。先做一些較為大路的分析，假定沒有 random effect ，到底年紀和性別和 dist 有沒有關係。

> crude.model < - lm(dist~age+gender,data=den.data)
> summary(crude.model)
Call:
lm(formula = dist ~ age + gender, data = den.data)
Residuals:
Min 1Q Median 3Q Max
-5.97760 -1.47760 -0.04983 1.20017 5.37795
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 15.37551 1.13070 13.60 < 2e-16 ***
age 0.66111 0.09794 6.75 8.39e-10 ***
gender 2.31321 0.44573 5.19 1.03e-06 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 2.276 on 105 degrees of freedom
Multiple R-squared: 0.4084, Adjusted R-squared: 0.3972
F-statistic: 36.25 on 2 and 105 DF, p-value: 1.072e-12

似乎年紀和性別都和 dist 有關。之後我們看看每個小朋友的 dist 與年齡增長的關係。 用圖了解最好。載入 R/S-PLUS 最有名的套件，叫做 lattice 。 ((這個 lattice 用過之後，會覺得 SPSS/SAS 的繪圖功能其實相當廢。))

> library(lattice)
> xyplot(dist~age|id, data=den.data, panel=function(x,y) {
panel.xyplot(x,y)
panel.lmline(x,y, lty=2)
panel.loess(x,y,span=2)}
)
圖會是這樣。

圖中的虛線是 regression line ，藍線是 lowess line 。見到年齡和 dist 基本上呈線性相關。圖中見到，每個小朋友的 slope 及 y-intercept 都好像有點不同。我們試圖再圖像化這些 slope 及 y-intercept 。

> library("nlme")
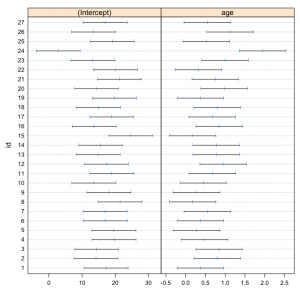
> dist.lmlist < - lmList(dist~age|id, data=den.data)
> plot(intervals(dist.lmlist))

我們先試試做一個 random intercept model 。

> lme.intercept < - lme(dist~age+gender, random=~1|id, data=den.data)
> summary(lme.intercept)
Linear mixed-effects model fit by REML
Data: den.data
AIC BIC logLik
448.1845 461.4543 -219.0922
Random effects:
Formula: ~1 | id
(Intercept) Residual
StdDev: 1.808471 1.437156
Fixed effects: dist ~ age + gender
Value Std.Error DF t-value p-value
(Intercept) 15.375505 0.8983718 80 17.114857 0.0000
age 0.661111 0.0618453 80 10.689749 0.0000
gender 2.313210 0.7621995 25 3.034914 0.0056
Correlation:
(Intr) age
age -0.757
gender -0.503 0.000
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.73209680 -0.54937001 -0.02397358 0.46412420 3.64348757
Number of Observations: 108
Number of Groups: 27
這個結果，其實只需看兩件事。第一件是隨機作用的 intercept ，我們只能獲得其 Standard deviation ((只是 Variance 的 SQRT)) 及 residual 的 standard deviation 。在 SPSS ((要 SPSS 11 以後才可以做 LME )) ，它能夠計出 Variance/SD 及 Variance 的 Standard Error ，繼而用 Wald's Z test 做假設檢定，了解 Variance 是否等於零。經過我多翻研究，發現 SPSS 的做法是有問題的。因為這個 Variance 是無從了解其 SE ，實在不知道它是怎樣的計出來。而且用 Z test 亦是相當有問題，因為我們根本不知道 Population 的 Variance 。我們只應用 t 。可是屆時又有問題。
第二件事是固定作用因素的假設檢定。 R 能夠計算出 t 值。但是那個 DF （ Degree of Freedom ）又是有問題。在 SPSS 或 SAS 的 PROC MIXED ，他們計出的 DF 會與 R 的有分別。 ((我的 SPSS 11 說 Age 的 DF 是 107.07 ，但 R 用更保守的 80 。用 SPSS 那個大 DF 可能會出現 False Positive 。)) 每個軟件計出來的 DF 都不同，或許是因為這個 DF 怎樣計出來都未有定案。據我所知，其實整件事都不應該有假設檢定。原因又是同一個問題：我們踏入了貝葉氏學派的領域。那些 DF 怎樣的計算都不會準。
我認為較為合適的方法，是比較 LME 和 OLS 的 model fit 。

> anova(lme.intercept,crude.model)
Model df AIC BIC logLik Test L.Ratio p-value
lme.intercept 1 5 448.1845 461.4543 -219.0922
crude.model 2 4 492.9212 503.5370 -242.4606 1 vs 2 46.73669 < .0001
似乎 random intercept model 比 crude model 更加 fit ，用到的檢定叫做 Likelihood ratio test 。這個 Likelihood ratio test 其實相當 liberal ，即是實際無分別都會話有分別。這裡要介紹一個數值，叫做赤池信息量準則（ AIC ）。這個東西比一般的 R-sq 更有用。 AIC 值愈小代表 model 更 fit 。要是兩個模型的 AIC 值只差 2 ，其實代表兩個 model 的分別不大。我們見到 lme.intercept 的 AIC 是 448.18 而 crude.model 是 492.92 ，大降了數十。似乎亦驗證了 likelihood ratio test 的結論。

之後我們要看看 random slope model 。

> lme.slope <- lme(dist~age+gender, random=~age|id, data=den.data)
> summary(lme.slope)
Linear mixed-effects model fit by REML
Data: den.data
AIC BIC logLik
450.0082 468.5859 -218.0041
Random effects:
Formula: ~age | id
Structure: General positive-definite, Log-Cholesky parametrization
StdDev Corr
(Intercept) 2.7805574 (Intr)
age 0.2244492 -0.762
Residual 1.3183183
Fixed effects: dist ~ age + gender
Value Std.Error DF t-value p-value
(Intercept) 15.479078 0.9454164 80 16.372763 0.0000
age 0.661111 0.0713041 80 9.271706 0.0000
gender 2.138431 0.7583160 25 2.819973 0.0093
Correlation:
(Intr) age
age -0.787
gender -0.475 0.000
Standardized Within-Group Residuals:
Min Q1 Med Q3 Max
-3.08089650 -0.45459660 0.01398283 0.44883675 3.87195586
Number of Observations: 108
Number of Groups: 27
正如剛才所說，任何的 p-value 都不可以信。我們又比比 random intercept 和 random slope 的 model fit 。

> anova(lme.intercept,lme.slope)
Model df AIC BIC logLik Test L.Ratio p-value
lme.intercept 1 5 448.1845 461.4543 -219.0922
lme.slope 2 7 450.0082 468.5859 -218.0041 1 vs 2 2.176270 0.3368
無論 Likelihood ratio test 或 AIC 都指出加入 random slope 無助於增加 model fit 。我們似乎應該只用 random slope model 。
但問題是，我們總要有些東西來 report 。雖說 lme 任何的假設檢定都不可信。但總要說服他人，當控制了（ adjust ） random slope 的問題，到底年紀和性別是否 dist 的 predictor 。由於我們踏入了貝葉斯的領域，我們只能用貝葉斯的思維模式，只不過會很難的說服 Journal reviewer/editor ，要知道他們的統計知識多半是半桶水。我們要用到一種叫做 Markov Chain Monte Carlo （ MCMC ） 方法，去模疑 LME 的 parameters 的 posterior distribution 。再從這個 posterior distribution 找出一個 95% CI 。 ((嚴格來說，這個東西叫做 Highest Probability Density Interval, HPDI)) 不明不要緊，看看就明。 ((由於用 nlme 套件製作的 LME 不能做 mcmcsample ，我們要用 lmer4 套件再製作過同一個 LME ，再進行 mcmcsample 。))

> library("lme4")
> lme.intercept.lmer <- lmer(dist~age+gender+(1|id),data=den.data)
> lme.intercept.lmer.mcmc <- mcmcsamp(lme.intercept.lmer , n = 10000)
> HPDinterval(lme.intercept.lmer.mcmc, prob=0.95)
$fixef
lower upper
(Intercept) 13.5590023 17.1801221
age 0.5127435 0.8104797
gender 1.2264384 3.3721721
attr(,"Probability")
[1] 0.95
$ST
lower upper
[1,] 0.3962793 0.8380072
attr(,"Probability")
[1] 0.95
$sigma
lower upper
[1,] 1.470141 2.060459
attr(,"Probability")
[1] 0.95

我們用 MCMC 方法，重新抽樣一萬次 ((你可以設定 mcmcsample 抽樣的次數，只需要改改 n 這個參數就可以。當然，抽樣次數愈多，計算愈久。但現在的電腦運算能力，一個簡單的模型，抽樣十萬次以內，都可以在數秒完成。)) ，再生成了 Posterior distribution ，用來計算 CI 。我們從 Posterior distribution 見到，固定作用的 Intercept, age, gender 的 95% CI 都沒有包括零，似乎三者在控制了 random slope 後都是 dist 的 predictor 。
從這個討論我們見到：

1. LME 與一般的 OLS 根本不能類比的混為一談
2. LME 的分析比 OLS 麻煩很多
3. 一般的統計軟件的 LME 結果，由其是當中的假設檢定根本不能相信。作為一個負責任的統計分析員需要了解他們怎樣的計出來。而不是盲信統計軟件的結果。

這個我研究了個多星期，總結出來的心得。如果你看得明，希望對你有用。更加詳細的討論可看看以下：

Bates D. lmer, p-values and all that.
R Wiki. Conservative ANOVA tables in lmer.

---

Powered by Jekyll and profdr theme