Werden wir Helden für einen Tag
Home | About | ArchivePoisson
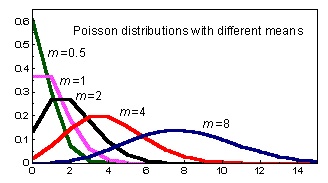
柏松分佈的機率質量函數
(Source: 美國地質調查局)
從梁博士 ((以前一直叫他梁生,現在叫梁博士)) 博客看到這篇刊登在自然的文章。
最近看到有人說「地震局說地震不能預測,為何餘震卻能預測」,去證明地震局根本就能預測地震。之前在一文的 footnote 已經加以討論。看過梁博士介紹的文,要加多兩筆。我是地理地質學白痴,以下純以統計學/機會率觀點解話。我是一個研究統計學/機率論的民間學者。
地震是一個隨機的事件。我們將時間分成一個個 Unit time ,或者 Time Interval ,例如一天、一年、十年。每個 Unit 都可能發生地震。假如將每個 Time Interval 的地震次數 Plot 出來,這就是著名的泊松分佈( Poisson Distribution )。地震是一個柏松過程 (Poisson Process)。柏松分佈不像常態分佈 ((常態分佈的 pmf 有兩個參數,分別是平均數和變異數。而泊松分佈的平均數及變異數均為 Lambda ,故此只有一個參數。)) ,其機率質量函數(Probability Mass function, pmf)只有一個參數,叫做 Lambda 。 Lambda 像常態分佈的平均數,是表達每一個 Time Interval 平均事件發生次數。我估計,地震的 Lambda 是相當細的。
常見的柏松分佈有甚麼呢?例如一個電話投訴中心每分鐘收到的電話次數、一台 Server 每天被入侵次數,又或者一個急症室每天因為交通意外入院的病人數字。這些過程都有一個共通點,就是一般時間不發生,每發生的話,就會發生多次。例如交通意外的例子,通常時間急症室每天都不會收到交通意外傷者。可是在一天之內出現第一名傷者,傷者通常多於一位。即是話,有第一位,就很有可能有第二位、第三位甚至第 N 位。難以預測的,是那一個 Time Interval 有第一位入院傷者。當這個 Time Interval 有第一位入院,出現 2-N 位的預測就會易很多。
統計學/機率論,不明白,不要緊。用係人都明的說法係:阿媽都知發生地震後會有餘震。發生了地震後,預測會發生餘震是最容易的投注。但不代表,預測第一因地震,同樣是容易的投注。